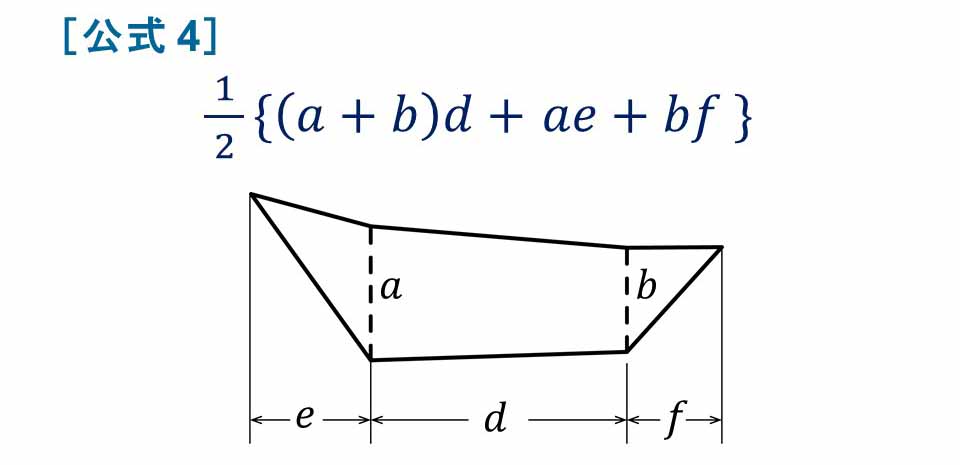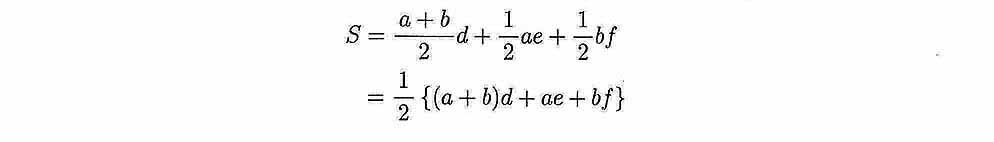付録（公式集）
土塁，土橋，堀などの体積計算に有用であった公式を挙げる．その証明 [西村 06] も示す．
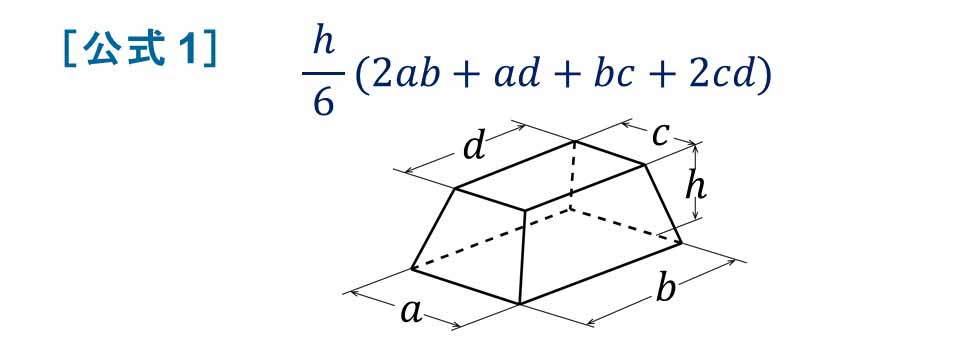
［公式 1］ 四角錐台の体積.
上下の底面が長方形で，対応する各辺（縦 a と c ; 横 b と d ）が並行であり， 高さ h の四角錐台（稜線は 1 点で交わらなくてもよい）（付図 1）の体積：
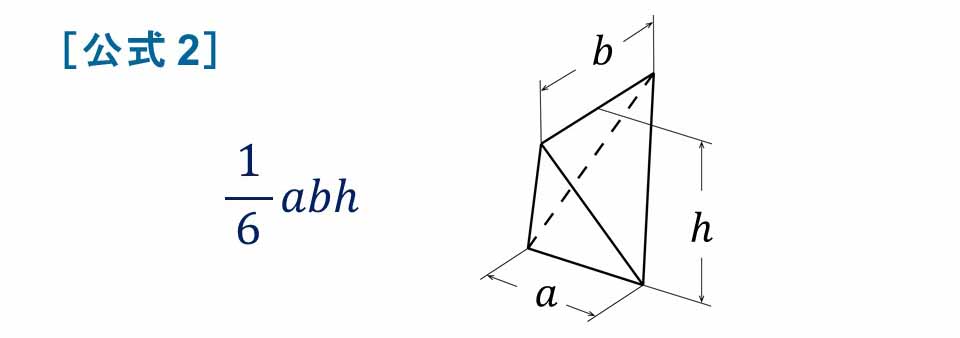
［公式 2］ 四面体の体積．
上下の辺（長さ a と b）がねじれの位置にあり，高さ h の四面体（付図 2）の体積：
付図 2. 四面体
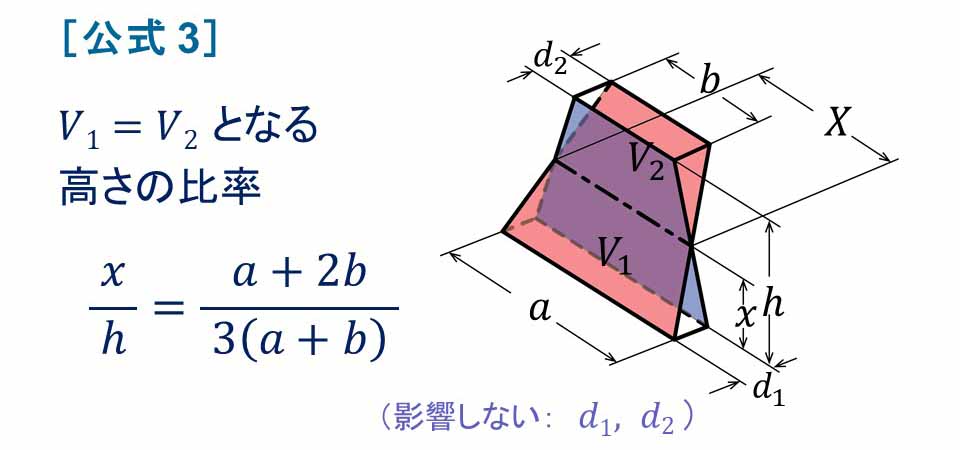
［公式 3］ くさび形の等積中心線．
事後の計算を簡略にするために，台形面内にあって底辺と平行な“等積中心線”の高さ（底辺からの距離）を求める． ここで定める“等積中心線”とは，台形内の底辺と平行な直線であって， それを中心として，台形面を面と垂直な方向に移動したときにできる上下のくさび形の立体の体積が等しくなる直線である（付図 3）． 台形の下底の長さを a，上底の長さを b，高さを h とすると，等積中心線の高さは：
付図 3. くさび形の等積中心線の位置
［公式 4］ 三角形＋台形＋三角形 の面積．
付図 4 は，よく現れる断面の形状である．便宜のために，その面積を示しておく．
付図 4. 三角形＋台形＋三角形 の面積
参考文献
[西村 06] 西村和夫「土塁の体積と土橋の体積」中世城郭研究会月例会, 2006-08-20.
